Before we explain what a linear pair postulate is, let’s first break down what exactly it means. In Geometry we use a number of different definitions to define certain truths. A postulate means that something is true beyond needing to be proven. Cambridge Dictionary uses the following definition for postulate:

to suggests or accept that a theory or idea is true as a starting point for reasoning or discussion…

Now that we’ve defined what postulate means, we now need to understand what a linear pair postulate means in geometry. A linear pair is simply two adjacent angles, that when added together, add up to 180 degrees. 180 degrees in this case ends up looking like a line (because it is). So let’s visually show this then:

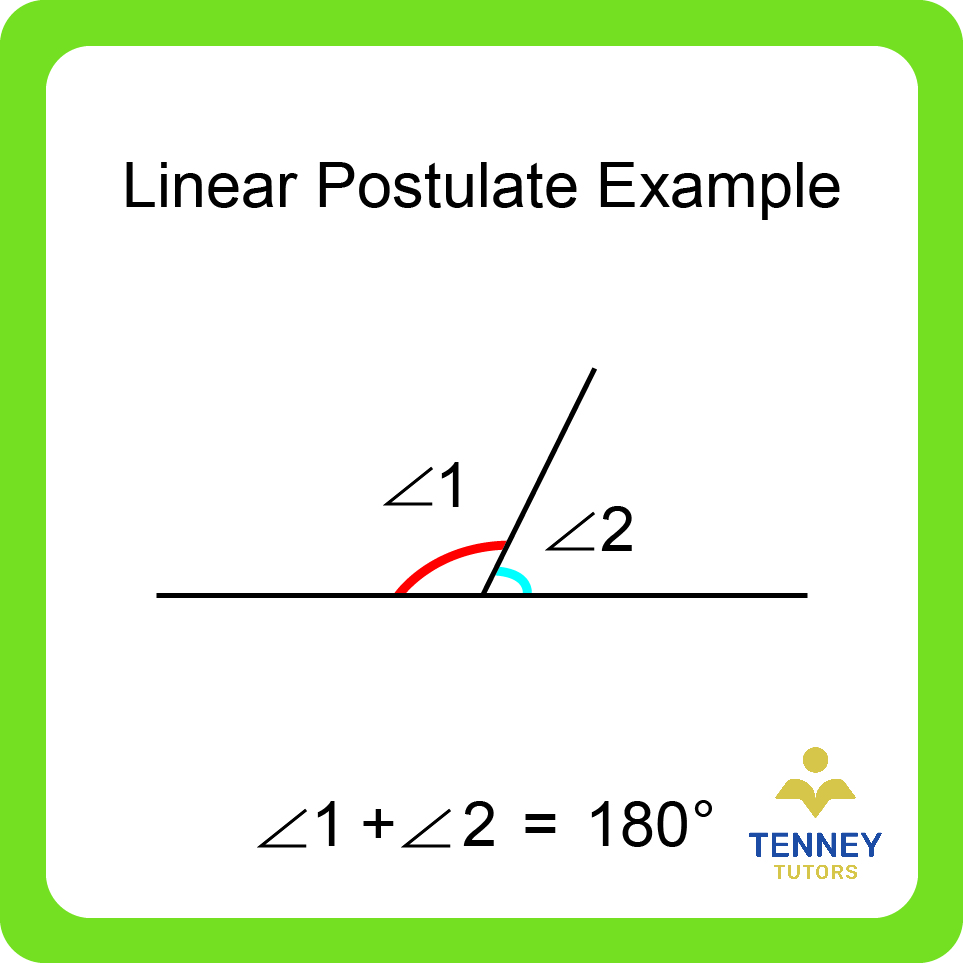
As you can see, in this example shown above, ∠1 and ∠2 add up to make 180°. While both angles are different, when combined they equate to a line which is why the postulate is defined as linear. (a straight line is 180°)

So how do you solve this then? Well in this example above, let’s say that ∠1 = 100°. Now let’s try to find what ∠2 is. Well knowing the linear postulate rule, we can determine that both angles add up to 180°. So in order to find what ∠2 is, we must do a little bit of algebra. Let’s subtract 100 from 180. This ends up being 80 which means that ∠2 must equal 80°.

Why Linear Pair Postulate Matters

Knowing how to use the postulate is the most important thing. It’s a key that can trivialize solving the sum of two linear angles. While the example above is simple, questions can become increasingly complex if the problem doesn’t outright give you the angle for one of the sides.

 

More advanced level questions will give you equations to solve for one or both angles that add an extra step of complexity. This can seem too difficult at first, which is why the linear pair postulate matters so much. Since you know both angles will always equal 180°, it’s easy to check your work as you solve both angles. If the sum of both angles does not equal 180°, then you should look over your work again for any errors.

Follow For More!

Be sure to check out our social media page for all the updates on TenneyTutors and our in person private school: The Tenney School!